Derivative of a sequence

2016-12-05

My colleagues were recently discussing the idea of taking the derivative of a sequence. For example, consider the Fibonacci sequence $F(n) = \begin{cases} 0 & n = 0 \\ 1 & n = 1 \\ F(n-1) + F(n-2) & n \ge 2 \end{cases}.$ What meaning can we assign to $\frac{\mathrm{d} F}{\mathrm{d} n}?$

My first instinct was that this is obviously a pointless exercise, since differentiation is inherently a limiting process. The best you could hope to do is a finite difference approach: $\left. \frac{\Delta F}{\Delta n} \right|_{n^+} = \frac{F(n+1) - F(n)}{(n+1) - n} = F(n+1) - F(n),$ but that's hardly interesting. It's also possible to make the sequence into a continuous function, whose derivative is then straightforward to calculate, but by doing so, I feel that you lose the nature of the sequence.

Chemical potential

It later occurred to me that I had seen something like this before. In thermodynamics, the chemical potential is defined as the change in internal energy with particle number: $\mu = \frac{\partial U}{\partial N}.$ The number of particles is an integer, so this appears to be similar to the above quantity. In fact, I had previously been perplexed by the presence of an infinitesimal change in particle number.

My mistake was forgetting that all values in thermodynamics are averages, so $N$ in that expression is not necessarily an integer. It is the average number of particles, and may very well be a fractional quantity. The above expression is more explicitly written as $\mu = \frac{\partial \langle U \rangle}{\partial \langle N \rangle},$ where the average internal energy is $\langle U \rangle = \sum_{i} p_i E_i$ and the average number of particles is $\langle N \rangle = \sum_{i} p_i N_i.$ I'm using $p_i$ to mean the probability of microstate $i$ to avoid all the business with writing out partition functions and Boltzmann factors.

We can apply this idea to taking the derivative of a sequence $F(n)$ with respect to $n$. Instead of the initial question, we ask about $\frac{\mathrm{d} \langle F \rangle}{\mathrm{d} \langle n \rangle},$ where $\langle F \rangle = \sum_{n=0}^\infty p_n F(n)$ and $\langle n \rangle = \sum_{n=0}^\infty p_n n.$ This requires us to have a probability distribution for the indices, so it's not a property of the sequence alone, but it is a concrete definition.

Fibonacci & Poisson

The simplest distribution with which to start is the Poisson distribution, with one parameter $\lambda$ and pmf $p_n = e^{-\lambda} \frac{\lambda^n}{n!}.$ This immediately gives us the simple expression $\langle n \rangle = \lambda.$ I don't know of anything as nice for $\langle F \rangle$, but we can calculate it numerically as a function of 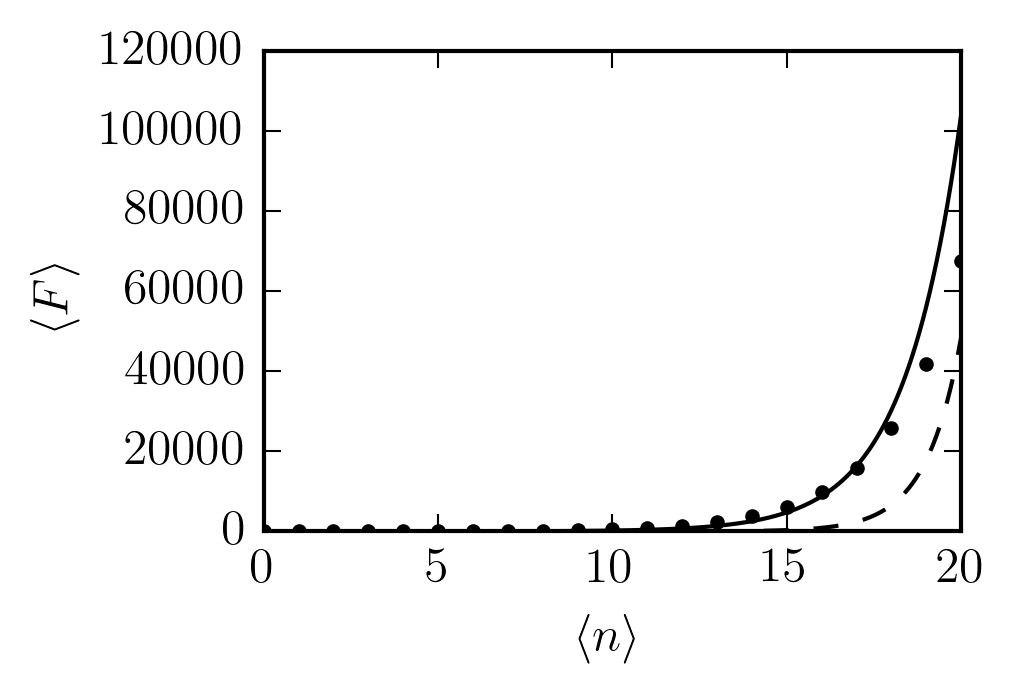$\langle n \rangle$: For comparison, $10 F(\langle n \rangle)$ is plotted with points and $\frac{e^{\langle n \rangle}}{10^4}$ is dashed. The variance of the distribution grows as $\langle n \rangle$, so we expect the average value to contain contributions from higher and higher values of $F(n)$, and it's not surprising that $\langle F \rangle$ increases much faster than $F(\langle n \rangle)$.

What about the derivative? Since $F(n+1) - F(n) = \begin{cases} 1 & n = 0 \\ F(n-1) & n \ge 1 \end{cases},$ we find that $\frac{\mathrm{d} \langle F \rangle}{\mathrm{d} \langle n \rangle} = p_0 + \sum_{n=1}^\infty p_n F(n-1),$ which looks like 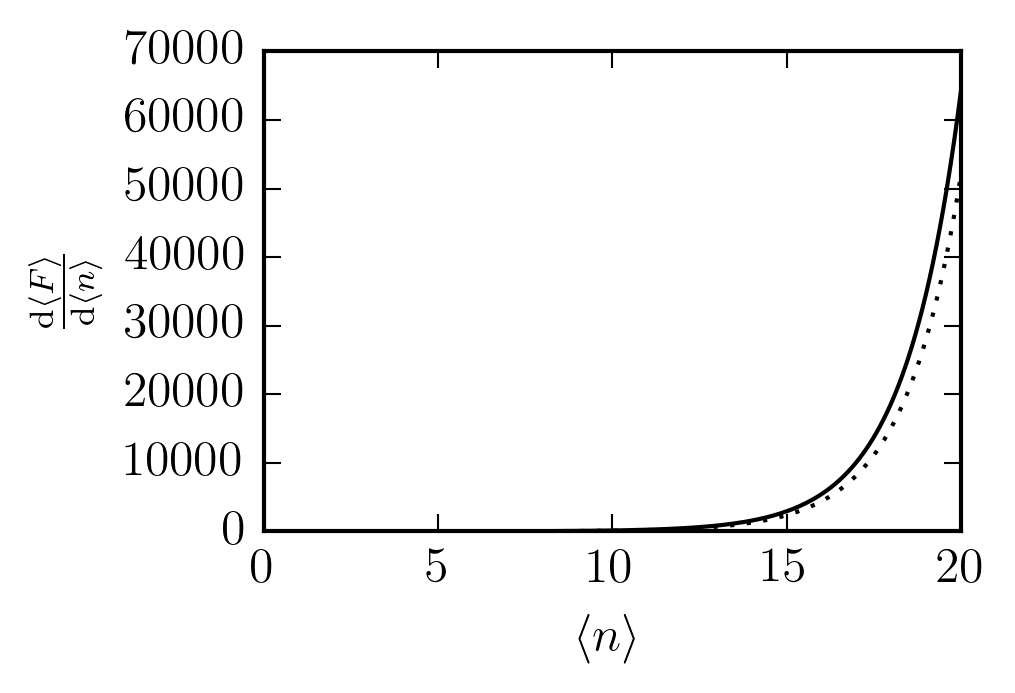For comparison, we also have (dotted) $\frac{\langle F \rangle}{2}.$ There's a degree of similarity, like what we might expect for an exponential function.

Fibonacci & geometric

The geometric distribution, with parameter $p$ and pmf $p_n = (1-p)^n p$ is quite different from the Poisson distribution, so let's see what effect this change has on the derivative. The mean value is $\langle n \rangle = \frac{1-p}{p}.$ Using the generating function for the Fibonacci sequence, we get the closed form expression $\langle F \rangle = p \frac{p - 1}{p^2 - 3 p + 1},$ which only holds for $1 - p < \frac{1}{\phi} \approx 0.61803,$ where $\phi$ is the golden ratio. This is equivalent to $p > \frac{\phi - 1}{\phi} \approx 0.38197,$ and $\langle n \rangle < \phi \approx 1.61803.$ At that point, the denominator of $\langle F \rangle$ vanishes and $\langle F \rangle$ diverges. Before that, we have

Application of the chain rule then gives us $\frac{\mathrm{d} \langle F \rangle}{\mathrm{d} \langle n \rangle} = p^2 \frac{2 p^2 - 2 p + 1}{(p^2 - 3 p + 1)^2}$ which looks like 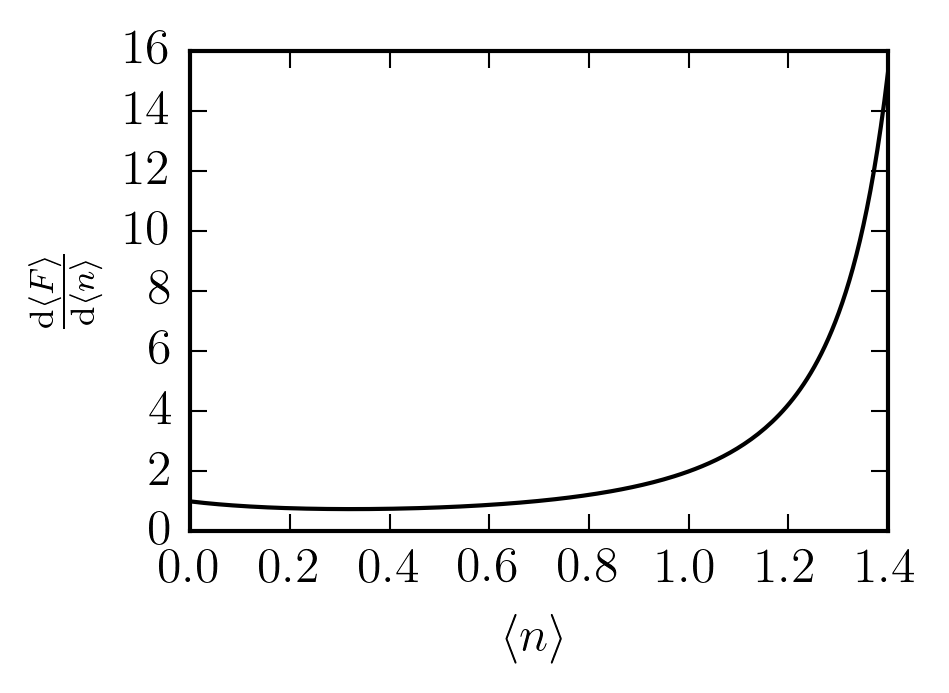Unlike the exponential behaviour we seemed to get with the Poisson distribution, this derivative behaves as a rational function.

Clearly, the behaviour of a single sequence can vary greatly under this operation depending on the choice of distribution. Unless one has a particular distribution already in mind (as in statistical mechanics), it's probably not a very useful approach for studying the sequence itself.