Matrix product states and Tucker decomposition

2019-11-15

By representing a quantum state $\ket{\psi}$ in a product basis $\{ \ket{\vec{n}} \}$, one obtains information about the state in the form of a rank-$L$ tensor: $C_{\vec{n}} = \ip{\vec{n}}{\psi} = \ip{n_1 \, n_2 \, \dots \, n_L}{\psi}.$ Here's what $C_{\vec{n}}$ looks like in dead bug form for $L = 8$ sites: If each local basis $\{ \ket{n_i} \}$ has dimension $d$ (corresponding to a single site, spin, orbital, mode, or whatever else you'd like), then this tensor has $d^L$ elements in total. Because exponential growth of this straightforward approach prevents the study of large systems, attempts have been made to reduce the total number of elements by decomposing $C_{\vec{n}}$ into several smaller tensors.

Two particularly successful examples of this are:

• matrix product states (MPSs), which are used in the density matrix renormalization group (DMRG), and which I've discussed before; and
• Tucker decomposition (TD), which appears in multiconfiguration time-dependent Hartree (MCTDH).

My goal in the following is to briefly demonstrate the surface differences between MPSs and TD (as well as the latter's hierarchical counterpart, HTD), with the aid of illustrations to elucidate the mathematics.

Matrix product states

The general expression for a matrix product state is $C^{\mathrm{MPS}}_{\vec{n}} = \sum_{\vec{\alpha}} A^{(1) \alpha_1}_{n_1} \left[ \prod_{i=2}^{L-1} A^{(i) \alpha_{i-1} \alpha_i}_{n_i} \right] A^{(L) \alpha_{L-1}}_{n_L}$ or $C^{\mathrm{MPS}}_{\vec{n}} = \sum_{\alpha_1=1}^m \sum_{\alpha_2=1}^m \cdots \sum_{\alpha_{L-1}=1}^m A^{(1) \alpha_1}_{n_1} A^{(2) \alpha_1 \alpha_2}_{n_2} \cdots A^{(L) \alpha_{L-1}}_{n_L},$ where the number of terms $m$ in each sum over $\alpha_i$ is known as the bond dimension. Exploiting the repeated matrix multiplication structure, we may also write $C^{\mathrm{MPS}}_{\vec{n}} = \vec{A}^{(1)}_{n_1} \vec{A}^{(2)}_{n_2} \cdots \vec{A}^{(L)}_{n_L},$ which is the form that gives this decomposition its name.

This may be expressed in the concrete case of $L = 8$ sites as The vertical lines are the physical indices $n_i$ (each running from 1 to $d$), while the horizontal lines are the bond indices $\alpha_i$ (from 1 to $m$). The tensor contractions (sums over $\alpha_i$) are indicated by linking the indices. It is important to point out that this is an inherently one-dimensional decomposition: each tensor is linked exclusively to adjacent tensors. It's therefore no surprise that MPSs appear in the heart of DMRG, which has been used extensively for finding ground states of one-dimensional systems.

The number of elements in this construct scales as $L d m^2$; if $m$ is constant, this is a drastic improvement over $d^L$! In fact, so long as $m$ is less than exponential in $L$ (which is the typical situation for one-dimensional systems), we should still gain from this decomposition when $L$ is sufficiently large.

Starting from a full tensor $C_{\vec{n}}$, it's possible to obtain the MPS form by repeated singular value decomposition (SVD). This is not commonly done in practice, but it can be used to prove that this decomposition is exact ($C^\mathrm{MPS}_{\vec{n}} = C_{\vec{n}}$) for some $m$ that's big enough. The SVD is used on smaller tensors in DMRG in order to control the size of the MPS by keeping only the largest $m$ singular values.

Tucker decomposition

Tucker decomposition of a tensor has the form $C^{\mathrm{TD}}_{\vec{n}} = \sum_{\vec{\alpha}} A_{\vec{\alpha}} \left[ \prod_{i=1}^L B^{(i) \alpha_i}_{n_i} \right]$ or $C^{\mathrm{TD}}_{\vec{n}} = \sum_{\alpha_1=1}^s \sum_{\alpha_2=1}^s \cdots \sum_{\alpha_L=1}^s A_{\alpha_1 \alpha_2 \cdots \alpha_L} B^{(1) \alpha_1}_{n_1} B^{(2) \alpha_2}_{n_2} \cdots B^{(L) \alpha_L}_{n_L},$ where $\vec{A}$ is the rank-$L$ core tensor, and each $\vec{B}^{(i)}$ is a rectangular matrix. Because each of the matrices shares an index with the core tensor, there is no linear-algebraic shorthand notation.

For $L = 8$ sites, we have 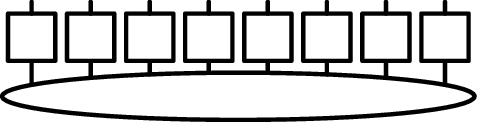In MCTDH terminology, the squares are the single-particle functions (SPFs), which project from the full $d$-dimensional one-site space spanned by the primitive basis $\{ \ket{n_i} \}$ to a relevant subspace of dimension $s$. It's obvious that the exact tensor may be recovered ($C^\mathrm{TD}_{\vec{n}} = C_{\vec{n}}$) when $s = d$ and each SPF is the identity operator.

The number of elements scales as $s^L + L d s$, growing exponentially with $L$. However, the hope is that $s$ can be much smaller than $d$, quelling the exponential growth a little bit. For many strictly one-dimensional systems, one doesn't expect this to be more compact than the MPS form (at least asymptotically). On the other hand, in the absence of any natural ordering to the sites (such as in two-dimensional systems or for vibrational modes), the bond dimension of an MPS could grow very rapidly with $L$, causing Tucker decomposition to fare much better in comparison.

In principle, Tucker decomposition of a tensor can be obtained via higher-order singular value decomposition (HOSVD). Though that's a bit of a misnomer, because the "core tensor" in a regular (matrix) SVD is the diagonal matrix of singular values, but the corresponding piece of the HOSVD is not diagonal in any sense.

Tucker decomposition with mode combination

In an effort to reduce the rank of the core tensor in Tucker decomposition, sites (modes) are sometimes combined together. This can be very beneficial for sites that are correlated and only live on a small subspace of their product space. This isn't fundamentally a different decomposition from plain TD, because it amounts to a relabelling of the primitive basis states, but it's still useful to take a peek at how it looks and feels.

The picture that we get for $L = 8$ when we group each pair of sites is 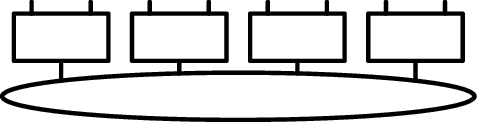Now the core tensor is only a rank-$4$ tensor! Of course, if each mode combination is a trivial one (a direct product index composed from the primitive indices), that's only an illusion and the core tensor simply reverts to $C_{\vec{n}}$ itself.

Counting the number of elements begins to get tricky, because there is now freedom in the structure of the decomposition. If we assume a homogeneous grouping of $K$ SPFs, each combining $L/K$ sites, we find that the number of elements scales as $s^K + K d^{L/K} s$, which is largely reminiscent of the uncombined version. The trade-off here is a larger exponent in the second term in exchange for a reduction of the exponent in the first term.

Hierarchical Tucker decomposition

A natural extension of the mode combination idea is to make it recursive. At this point, the index wrangling gets quite unpleasant, especially if we want to be comprehensive, and it's quite frankly unnecessary for our purposes. Instead, we'll try to remain comprehensible and just draw an example of hierarchical Tucker decomposition (HTD) for $L = 8$, where we've paired up two indices at each layer of the hierarchy, making a perfect binary tree:

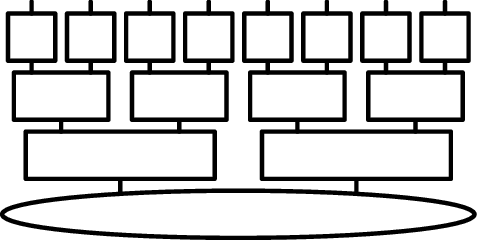
More generally, HTD may include tensors all sorts of shapes and sizes, and choosing how to structure it is not a trivial endeavour. In 2003, Wang and Thoss showed how to apply the usual MCTDH algorithms recursively to such a tree structure of tensors in multilayer multiconfiguration time-dependent Hartree (ML-MCTDH).

To count the elements, we'll assume a perfect binary tree shape, which will have $2 L - 1$ tensors spread across $1 + \log_2 L$ layers. This implies a certain pattern in the problem (imagine splitting a two-dimensional lattice in half recursively), which will not always be present, so this isn't the most general form, but it's easy to analyze. If the interior indices have dimension $s$, we find that the total number of elements is $(L - 2) s^3 + s^2 + L d s$. As long as $s$ is less than exponential in $L$, we have no exponential terms!

Summary

Matrix product states (used in DMRG) and Tucker decompositions of all flavours (used in MCTDH) have some features in common: they are more compact than the full tensor that they approximate, and they can be made arbitrarily exact. (As promised, this was only a shallow inspection!) However, they also have some qualitative differences, and I hope that these are evident in the above diagrams.

The most important disparity is the presence of a core tensor in TD, compared to the decentralized nature of MPSs. The latter exploit the natural ordering of a one-dimensional system, while the former may also be freely applied to other geometries.

Plain Tucker decomposition and TD with mode combination will still have an exponentially-growing number of elements as one grows the system, while a matrix product state (when applied in an appropriate situation) will not. Hierarchical Tucker decomposition is also capable of sub-exponential scaling, and, unlike an MPS, it is not inherently limited to one-dimensional systems. Here are some scaling formulas all in one table: