Exponentially-spaced integers

It's often useful to have exponentially-spaced integers, so that they are evenly distributed when plotted on a logarithmic scale. The simplest way to generate them is to exponentiate linearly-spaced numbers and then round:

1
2
3

julia> round.(Int, exp.(0:7))'
1×8 LinearAlgebra.Adjoint{Int64,Array{Int64,1}}:
 1  3  7  20  55  148  403  1097

Past the first decade, which is significantly rounded, these integers are perfectly spaced: However, they're not very familiar to most people, and it's possible for the rounding step to produce duplicates, making them potentially tricky to generate. If you're willing to sacrifice the spacing a little more, I want to show you why integers of the form $m \cdot 2^k$ can be a very convenient alternative.

Powers of two

Some of the nicest exponentially-spaced integers around are the powers of two, which are trivial to generate and easily recognizable: Such elegance!

Filling in the gaps

If $2^k$ is sufficient for your purposes, I'm not sure why you're even here. But what if the spacing is a bit too large? The jump from $512$ to $1024$ is quite a big one, and $1024$ could be beyond your capabilities. Maybe you're looking for something more in line with your budget.

Logarithmically speaking, the closest integer to the halfway point between $512$ and $1024$ is $724$, but there's a good chance that I had never encountered this number in my entire life until I computed it for this purpose. I don't know anything about it. How can I trust it?

No, that won't do. Instead, we'll cheat a little bit and use $768$. That really takes me back! What a nice, dependable integer. It turns out that $768 = \frac{3}{2} 512 = 3 \cdot 2^8,$ since $3/2$ is the average of $1$ and $2$. Thus, in addition to the powers of two, $1 \cdot 2^k = 1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024, \dots,$ we can also use powers of two multiplied by three: $3 \cdot 2^k = 3, 6, 12, 24, 48, 96, 192, 384, 768, 1536, \dots.$ A clean source of unlimited numbers!

Less flippantly, integers with large prime factors, like $724 = 2^2 \cdot 181$, are unfavourable for some algorithms. For example, certain FFT algorithms fare better on arrays whose sizes have small prime factors. Thus, there are applications for which it's better to use numbers purposely constructed from small factors.

Let's visualize the amount of imperfection in the layout of these additional numbers. If we draw two octaves (say, from $256$ to $1024$, although the actual values don't matter), we get three powers of two ($2^k$, $2^{k+1}$, $2^{k+2}$): In linear space (filled), the distances between them are uneven (one is twice the other), but in log space (hollow), they are properly spaced. If we add in the fillers $3 \cdot 2^{k-1}$ and $3 \cdot 2^k$, we see that they are nicely located in the middle of each octave when viewed linearly, but are slightly off-kilter logarithmically: This is the price to be paid for having such pleasant numbers to work with.

Ad nauseam

There's no reason to stop there, of course. In addition to dividing the interval from $1$ to $2$ into two segments using $3/2$, we could split each of those further with $5/4$ and $7/4$, making a total of four segments. The first of these fractions gives us $5 \cdot 2^k = 5, 10, 20, 40, 80, 160, 320, 640, 1280, \dots,$ whose inclusion looks like The second one results in $7 \cdot 2^k = 7, 14, 28, 56, 112, 224, 448, 896, 1792, \dots,$ and completes this round of filling:

Using $m \cdot 2^k$ with $m = 1, 3, 5, 7$, we have obtained integers that are locally spaced linearly, and are therefore convenient to handle, but are globally spaced logarithmically, and therefore span many orders of magnitude. Naturally, the next round would be based on $9/8$, $11/8$, $13/8$, and $15/8$, yielding $m = 9, 11, 13, 15$ for a total of eight values per octave, but it's usually not necessary to go that far.

Jumping ahead

Before I leave you alone to ponder the usefulness of this approach, I'd like to point out one practical consideration. If you're interested in exponentially-growing quantities, it can be detrimental to have all sorts of small values running around underfoot. For example, using $m = 1, 3, 5, 7$ and starting at $8$, we get $8, 10, 12, 14, 16, \dots,$ which are consecutive even integers. We didn't do all that work just to end up generating even numbers!

To remedy this, you can stagger the start of each sequence. For example, if the gap between $8$ and $16$ is sufficiently small, but grows too large after that point, the $m = 3$ sequence can be started at $24$ instead of $12$. Then, if $16$ and $24$ and $32$ are close enough, the $m = 5$ and $7$ sequences can be started at $40$ and $56$, respectively, instead of $20$ and $28$. The staggered start allows us to tidy this (on a linear scale): 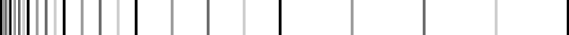into this: 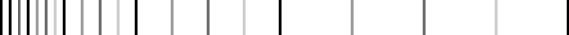Much better! The improved variant starts out linear for the first few octaves, but automatically switches to exponential spacing beyond that.