DMRG from a diagonalization perspective

There are many excellent descriptions of the density matrix renormalization group (DMRG), but they all seem to either explain it the old-school way (from a renormalization perspective, talking about blocks) or the newfangled way (from a matrix product state (MPS) perspective, talking about orthogonality centres). Both approaches are valid and insightful, but they tend to place all their focus on the mechanics of sweeps and other minutiae. These approaches shove the diagonalization step to the back of a cupboard, and the reader only gets a glance of it when they reach in to get some plates for the SVD truncation step.

Since my flow towards the DMRG fixed point in the space of quantum mechanical methods has been from the side of iterative methods, my understanding of it is also very much centred on the diagonalization step. For those of you in the same boat, I offer my explanation of how to reach that nearby shore where everybody runs quickly and primarily in one dimension.

Plain iteration

As an example, let's take the one-dimensional transverse field Ising model at the critical value of the parameters. For three sites with open boundary conditions, the Hamiltonian is just $\hat{H} = -\sigma^z_1 \sigma^z_2 - \sigma^z_2 \sigma^z_3 - \sigma^x_1 - \sigma^x_2 - \sigma^x_3,$ which has the matrix representation $\begin{pmatrix} -2 & -1 & -1 & 0 & -1 & 0 & 0 & 0 \\ -1 & 0 & 0 & -1 & 0 & -1 & 0 & 0 \\ -1 & 0 & 2 & -1 & 0 & 0 & -1 & 0 \\ 0 & -1 & -1 & 0 & 0 & 0 & 0 & -1 \\ -1 & 0 & 0 & 0 & 0 & -1 & -1 & 0 \\ 0 & -1 & 0 & 0 & -1 & 2 & 0 & -1 \\ 0 & 0 & -1 & 0 & -1 & 0 & 0 & -1 \\ 0 & 0 & 0 & -1 & 0 & -1 & -1 & -2 \end{pmatrix}$ in the standard basis $\{ |000\rangle, |001\rangle, |010\rangle, \cdots, |111\rangle \}$.

To find the ground state of this Hamiltonian, we can use an iterative solver, like Julia's eigs (which as of this writing (Julia 0.6.2) calls the venerable ARPACK under the hood):

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17

julia> H = [-2 -1 -1 0 -1 0 0 0; -1 0 0 -1 0 -1 0 0;
            -1 0 2 -1 0 0 -1 0; 0 -1 -1 0 0 0 0 -1;
            -1 0 0 0 0 -1 -1 0; 0 -1 0 0 -1 2 0 -1;
            0 0 -1 0 -1 0 0 -1; 0 0 0 -1 0 -1 -1 -2];
julia> E, psi = eigs(H; nev=1, which=:SR)[1:2];
julia> E[1]
-3.493959207434933
julia> psi[:,1]
8-element Array{Float64,1}:
 0.532481
 0.295505
 0.204495
 0.295505
 0.295505
 0.204495
 0.295505
 0.532481

That is, the ground state eigenvector $|\Psi\rangle$ is $\begin{pmatrix} 0.532481 \\ 0.295505 \\ 0.204495 \\ 0.295505 \\ 0.295505 \\ 0.204495 \\ 0.295505 \\ 0.532481 \end{pmatrix}$ with eigenvalue $E = -3.49396$. This is consistent with the formula $1 - \csc{\frac{\pi}{4L + 2}}$ for $L = 3$ sites.

There's a fairly small bound on what you can do with such a brute force approach. You know, the curse of dimensionality, exponential scaling, and all that. That's not to say that it doesn't have its uses, but at some point you won't even be able fit your wavefunction in memory anymore.

Projected iteration

But never mind all that negative blather! We'll stick with iterative diagonalization for the time being, and we'll give it a twist.

Suppose we already know half of the elements of the normalized eigenvector: $\begin{pmatrix} ? \\ ? \\ ? \\ ? \\ 0.295505 \\ 0.204495 \\ 0.295505 \\ 0.532481 \end{pmatrix}.$ Maybe they fell off a truck. I know a guy can get us more. And now that you've got your suspension of disbelief all fired up, I'll need you to look past the fact that the missing elements are dictated by symmetry.

One thing we absolutely can't do is take only the elements of the Hamiltonian from the remaining subspace and diagonalize that:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13

julia> H[1:4,1:4]
4×4 Array{Int64,2}:
 -2  -1  -1   0
 -1   0   0  -1
 -1   0   2  -1
  0  -1  -1   0
julia> E_sub, psi_sub = eigs(H[1:4,1:4]; nev=1, which=:SR)[1:2];
julia> psi_sub[:,1]
4-element Array{Float64,1}:
 0.857813
 0.398113
 0.22985
 0.22985

Even without compensating for normalization, we can see that this is not correct. It couldn't possibly be correct, since we have neglected the coupling between the two subspaces: $\begin{pmatrix} & & & & -1 & 0 & 0 & 0 \\ & & & & 0 & -1 & 0 & 0 \\ & & & & 0 & 0 & -1 & 0 \\ & & & & 0 & 0 & 0 & -1 \\ -1 & 0 & 0 & 0 & & & & \\ 0 & -1 & 0 & 0 & & & & \\ 0 & 0 & -1 & 0 & & & & \\ 0 & 0 & 0 & -1 & & & & \end{pmatrix}$ It doesn't look like much, but it's essential!

What we need is an effective Hamiltonian that knows about the known elements. We can't get rid of the last four states altogether, but we can replace that four-dimensional subspace with a one-dimensional one. That is, we're going to change our basis from the standard basis to $\{ |000\rangle, |001\rangle, |010\rangle, |011\rangle, |\phi\rangle \}$, where $|\phi\rangle$ has the (standard basis) representation $\frac{1}{\mathcal{N}} \begin{pmatrix} 0 \\ 0 \\ 0 \\ 0 \\ 0.295505 \\ 0.204495 \\ 0.295505 \\ 0.532481 \end{pmatrix}.$ The $\mathcal{N}$ is just there to keep things normalized. This new basis isn't a basis of the full Hilbert space, so we can't represent every possible state, but the subspace that it spans contains the ground state, so we're going to be just fine. In fact, we know that the ground state has the form $c_{000} |000\rangle + c_{001} |001\rangle + c_{010} |010\rangle + c_{011} |011\rangle + \mathcal{N} |\phi\rangle,$ where $c_{000}^2 + c_{001}^2 + c_{010}^2 + c_{011}^2 = 1 - \mathcal{N}^2$.

Because the subspace we're projecting onto is smaller than the full space, the transformation $\hat{T}$ between the two is isometric, but not unitary: $\begin{pmatrix} 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & \frac{0.295505}{\mathcal{N}} & \frac{0.204495}{\mathcal{N}} & \frac{0.295505}{\mathcal{N}} & \frac{0.532481}{\mathcal{N}} \end{pmatrix}^\dagger.$ This satisfies $\hat{T}^\dagger \hat{T} = \hat{1}$ (for a $5 \times 5$ identity), but $\hat{T} \hat{T}^\dagger \ne \hat{1}$ (for an $8 \times 8$ identity):

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

julia> T = zeros(8, 5);
julia> T[1:4,1:4] = eye(4);
julia> T[5:8,5] = psi[5:8,1]/norm(psi[5:8,1]);
julia> T
8×5 Array{Float64,2}:
 1.0  0.0  0.0  0.0  0.0     
 0.0  1.0  0.0  0.0  0.0     
 0.0  0.0  1.0  0.0  0.0     
 0.0  0.0  0.0  1.0  0.0     
 0.0  0.0  0.0  0.0  0.417907
 0.0  0.0  0.0  0.0  0.2892  
 0.0  0.0  0.0  0.0  0.417907
 0.0  0.0  0.0  0.0  0.753042
julia> T'*T
5×5 Array{Float64,2}:
 1.0  0.0  0.0  0.0  0.0
 0.0  1.0  0.0  0.0  0.0
 0.0  0.0  1.0  0.0  0.0
 0.0  0.0  0.0  1.0  0.0
 0.0  0.0  0.0  0.0  1.0
julia> T*T'
8×8 Array{Float64,2}:
 1.0  0.0  0.0  0.0  0.0       0.0        0.0       0.0     
 0.0  1.0  0.0  0.0  0.0       0.0        0.0       0.0     
 0.0  0.0  1.0  0.0  0.0       0.0        0.0       0.0     
 0.0  0.0  0.0  1.0  0.0       0.0        0.0       0.0     
 0.0  0.0  0.0  0.0  0.174646  0.120859   0.174646  0.314701
 0.0  0.0  0.0  0.0  0.120859  0.0836368  0.120859  0.21778 
 0.0  0.0  0.0  0.0  0.174646  0.120859   0.174646  0.314701
 0.0  0.0  0.0  0.0  0.314701  0.21778    0.314701  0.567072

The reason for this is that the transformation is lossless from the small basis to the large one (because we're guaranteed to start from the right subspace), but lossy in the other direction (because we might start outside the subspace). A direct consequence of this is that $\hat{T} \hat{T}^\dagger |\Omega\rangle \ne |\Omega\rangle$ for a general state $|\Omega\rangle$.

However, $\hat{T} \hat{T}^\dagger$ has an interesting form: it's still an identity in the first four elements, but the bottom-right corner is dense. That corner is simply the projector onto $|\Psi\rangle$ for the last four dimensions:

1
2
3
4
5
6

julia> (2psi*psi')[5:8,5:8]
4×4 Array{Float64,2}:
 0.174646  0.120859   0.174646  0.314701
 0.120859  0.0836368  0.120859  0.21778 
 0.174646  0.120859   0.174646  0.314701
 0.314701  0.21778    0.314701  0.567072

Because $|\Psi\rangle$ is invariant under both identity and projection onto itself, we have the useful expression $\hat{T} \hat{T}^\dagger |\Psi\rangle = |\Psi\rangle.$ We can see how the $\hat{T}^\dagger$ operator folds the bottom 4 elements of this vector into a single element (the element happens to be $1/\sqrt{2}$, because normalization is the key to success):

1
2
3
4
5
6
7

julia> T'*psi[:,1]
5-element Array{Float64,1}:
 0.532481
 0.295505
 0.204495
 0.295505
 0.707107

The $\hat{T}$ operator then unfolds the same elements correctly:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10

julia> T*T'*psi[:,1]
8-element Array{Float64,1}:
 0.532481
 0.295505
 0.204495
 0.295505
 0.295505
 0.204495
 0.295505
 0.532481

Using this operator, we can project the Hamiltonian to get $\hat{H} \to \hat{T}^\dagger \hat{H} \hat{T}$ with matrix elements $\begin{pmatrix} -2 & -1 & -1 & 0 & -0.417907 \\ -1 & 0 & 0 & -1 & -0.2892 \\ -1 & 0 & 2 & -1 & -0.417907 \\ 0 & -1 & -1 & 0 & -0.753042 \\ -0.417907 & -0.2892 & -0.417907 & -0.753042 & -2.62284 \end{pmatrix}.$ We've preserved the top-left corner, but we've compressed the bottom-right corner into a single value, and most importantly we've compressed the coupling between the two into some strange numbers. The real magic happens when we diagonalize this new (smaller) Hamiltonian:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20

julia> E_small, psi_small = eigs(T'*H*T; nev=1, which=:SR)[1:2];
julia> E_small[1]
-3.493959207434934
julia> psi_small[:,1]
5-element Array{Float64,1}:
 0.532481
 0.295505
 0.204495
 0.295505
 0.707107
julia> T*psi_small[:,1]
8-element Array{Float64,1}:
 0.532481
 0.295505
 0.204495
 0.295505
 0.295505
 0.204495
 0.295505
 0.532481

The eigenvalue is correct, and if we call $|\Psi'\rangle$ the ground state eigenvector of $\hat{T}^\dagger \hat{H} \hat{T}$, then $|\Psi\rangle = \hat{T} |\Psi'\rangle$. This should come as no surprise, since $\hat{H} |\Psi\rangle = E |\Psi\rangle$ implies that $\hat{T}^\dagger \hat{H} \hat{T} (\hat{T}^\dagger |\Psi\rangle) = E (\hat{T}^\dagger |\Psi\rangle),$ so $(\hat{T}^\dagger \hat{H} \hat{T}) |\Psi'\rangle = E |\Psi'\rangle,$ where $|\Psi'\rangle = \hat{T}^\dagger |\Psi\rangle$ and therefore $|\Psi\rangle = \hat{T} |\Psi'\rangle.$ The takeaway message here is painfully obvious: if you project a Hamiltonian onto a subspace that contains its ground state, you can still recover the ground state.

Iterated iteration (part 1)

Let's continue solving the same Hamiltonian, but this time more realistically. We're no longer going to assume any a priori knowledge of the wavefunction. The trial wavefunction $\frac{1}{\sqrt{8}} \begin{pmatrix} 1 \\ 1 \\ 1 \\ 1 \\ 1 \\ 1 \\ 1 \\ 1 \end{pmatrix} = \begin{pmatrix} 0.353553 \\ 0.353553 \\ 0.353553 \\ 0.353553 \\ 0.353553 \\ 0.353553 \\ 0.353553 \\ 0.353553 \end{pmatrix}$ is a fairly unbiased guess, so we'll start there. Its energy expectation value is not too far from the ground state energy, but there's room for improvement:

1
2
3

julia> psi0 = ones(8)/sqrt(8);
julia> dot(psi0, H*psi0)
-2.9999999999999996

The simplest way to deface this guess is to remove an element: $\begin{pmatrix} ? \\ 0.353553 \\ 0.353553 \\ 0.353553 \\ 0.353553 \\ 0.353553 \\ 0.353553 \\ 0.353553 \end{pmatrix}.$ We'd like to fill in the removed element with something dictated by the Hamiltonian. As you might expect, we'll rotate the Hamiltonian into a two-dimensional basis (containing $|000\rangle$ and some weird superposition of the others), diagonalize it there, and then put the resulting element in the vacant slot (while possibly renormalizing the rest). We hope that this will get us closer to the ground state.

Except the above explanation for why this trick should work relies on the result being an eigenstate of the Hamiltonian, and there's no way that's going to spontaneously pop out of our guess. After all, we're no longer projecting onto a space that we expect to contain the ground state. So what will we get? Let's try it out:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22

julia> T1 = zeros(8, 2);
julia> T1[1,1] = 1;
julia> T1[2:8,2] = psi0[2:8]/norm(psi0[2:8]);
julia> E_small1, psi_small1 = eigs(T1'*H*T1; nev=1, which=:SR)[1:2];
julia> E_small1[1]
-3.2857142857142847
julia> psi_small1[:,1]
2-element Array{Float64,1}:
 0.661438
 0.75    
julia> psi1 = T1*psi_small1[:,1]
8-element Array{Float64,1}:
 0.661438
 0.283473
 0.283473
 0.283473
 0.283473
 0.283473
 0.283473
 0.283473
julia> dot(psi1, H*psi1)
-3.2857142857142856

We've significantly improved the energy expectation value of our guess!

Interestingly, we observe that the eigenvalue $E_1$ of $\hat{T}_1^\dagger \hat{H} \hat{T}_1$ corresponding to $|\Psi_1'\rangle$ is the same as the energy expectation value of $\hat{H}$ with respect to $|\Psi_1\rangle = \hat{T} |\Psi_1'\rangle$. Or perhaps not so interestingly, if we take a look at how the sausage is made: $\langle\Psi_1|\hat{H}|\Psi_1\rangle = \langle\Psi_1'|\hat{T}^\dagger\hat{H}\hat{T}|\Psi_1'\rangle = \langle\Psi_1'|E_1|\Psi_1'\rangle = E_1.$

Interlude: Variational method

What we just saw was an application of the familiar variational method, albeit in an unusual form. In my experience, the variational method is typically applied when the Hilbert space in question is infinite-dimensional, which is the case even for the humble harmonic oscillator. One typically makes several calculations at different basis truncations and looks for convergence of the property of interest. When the property is deemed to be converged to within some tolerance, one can be confident that all the important basis states are being kept.

The usual frame of mind when dealing in such a truncated basis is that the removed states simply don't exist. For example, I might write down the creation operator $\hat{a}^\dagger$ in the basis of the first four harmonic oscillator eigenstates ($|0\rangle$ to $|3\rangle$) as $\begin{pmatrix} 0 & 0 & 0 & 0 \\ \sqrt{1} & 0 & 0 & 0 \\ 0 & \sqrt{2} & 0 & 0 \\ 0 & 0 & \sqrt{3} & 0 \end{pmatrix}.$ A direct consequence of this is that $\hat{a}^\dagger |3\rangle$ vanishes! It must, since there is no $|4\rangle$ state for it to go to. However, if I write down an arbitrary state $\frac{1}{2} \begin{pmatrix} 1 \\ 1 \\ 1 \\ 1 \end{pmatrix}$ in this truncated basis, there is something that's not being stated explicitly, but is important to consider: the infinitely many elements of this vector that have been removed on account of being irrelevant are implicitly set to zero: $\frac{1}{2} \begin{pmatrix} 1 \\ 1 \\ 1 \\ 1 \\ 0 \\ 0 \\ \vdots \end{pmatrix}.$

Any time we use the variational method like this, we're working in a subspace of the full Hilbert space where the abandoned elements have been zeroed out. That means that we can think of the matrix above as actually representing the operator $\hat{T}^\dagger \hat{a}^\dagger \hat{T}$, where $\hat{T}$ has the representation $\begin{pmatrix} 1 & 0 & 0 & 0 & 0 & 0 & \cdots \\ 0 & 1 & 0 & 0 & 0 & 0 & \cdots \\ 0 & 0 & 1 & 0 & 0 & 0 & \cdots \\ 0 & 0 & 0 & 1 & 0 & 0 & \cdots \end{pmatrix}^\dagger.$

Of course we're not required to set the coefficients of the orthogonal space to zero; we can choose whatever vector we want in that space. If your neglected coefficients are not negligible, you're going to get a very poor result from the point of view of basis truncation, but maybe that's fine for your use case. Crucially, no matter which vector we select, the variational principle still holds: the energy expectation value of every state $|\Omega\rangle$ in the corresponding subspace must be at least as large as the ground state energy: $\langle\Omega|\hat{H}|\Omega\rangle \ge E.$ There must also be at least one state in each subspace that minimizes this expectation value, so if we can find it, we will lower our estimate of the ground state energy.

Iterated iteration (part 2)

We can now take the idea of gradual improvement and roll with it. We'll keep taking one basis state at a time and projecting the Hamiltonian onto the subspace where the remaining elements are fixed. That would look something like this, where we sweep up and down the list of vector elements 20 times:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

julia> function make_T(v, i)
           T = zeros(length(v), 2)
           T[i,1] = 1
           N = norm(v[[1:i-1; i+1:end]])
           T[1:i-1,2] = v[1:i-1]/N
           T[i+1:end,2] = v[i+1:end]/N
           T
       end;
julia> function improve(H, T)
           E, psi = eigs(T'*H*T; nev=1, which=:SR)[1:2]
           E[1], T*psi[:,1]
       end;
julia> E_iter = dot(psi0, H*psi0)
-2.9999999999999996
julia> psi_iter = psi0;
julia> for _ in 1:20
           for i in [1:7; 8:-1:2]
               E_iter, psi_iter = improve(H, make_T(psi_iter, i))
           end
       end
julia> E_iter
-3.4939592074349344
julia> psi_iter
8-element Array{Float64,1}:
 0.532481
 0.295505
 0.204495
 0.295505
 0.295505
 0.204495
 0.295505
 0.532481

This result is perfect, and all we ever diagonalized were $2 \times 2$ matrices!

Here's what the energy looks like as a function of iteration step for the first few steps: 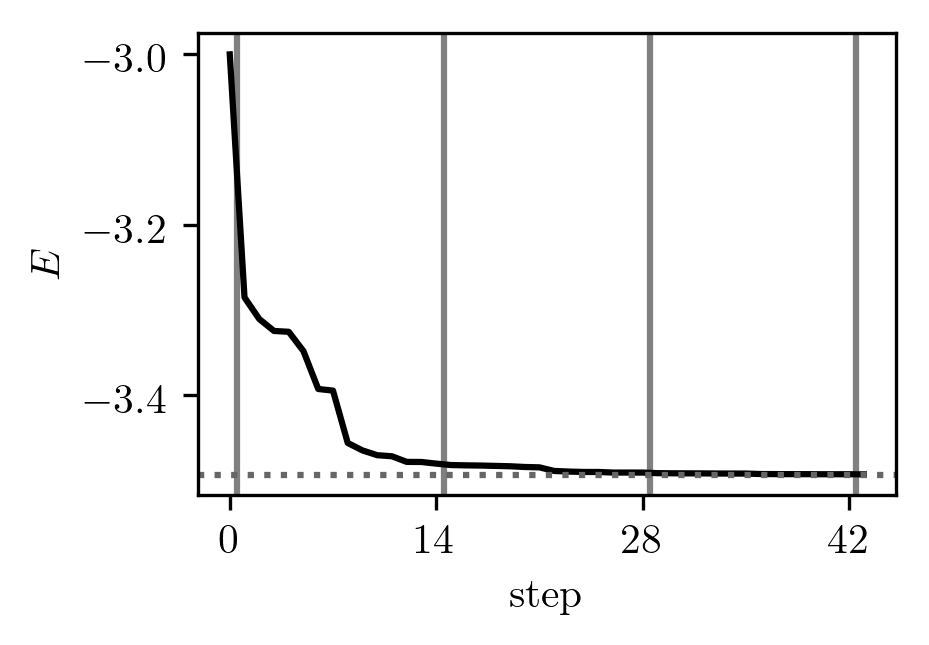The dotted horizontal line is the true ground state energy and the vertical lines demarcate the sweeps. On a log scale, we can see that the error in the energy decays exponentially: 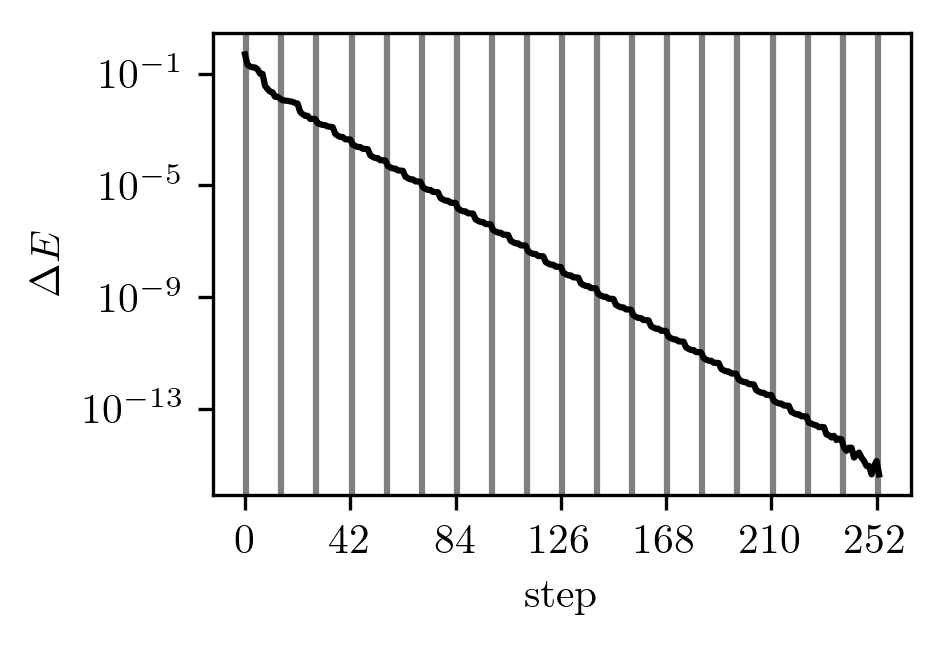The largest drops are always at the turning points, each time we finish going over all the elements again. We can improve the exponential drop-off, for example by considering two elements at once and by splitting the orthogonal subspace into two (one for the elements below the fixed ones and one for those above): 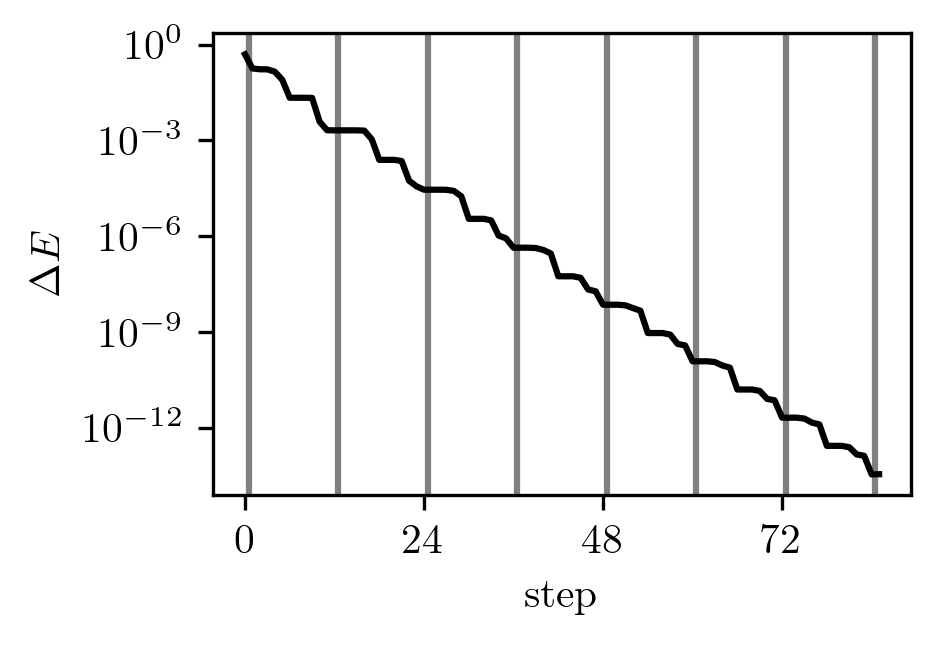In this case, we have to diagonalize $4 \times 4$ matrices, but the convergence rate is much better.

Interlude: Guaranteed convergence

Although this method is completely impractical for a number of reasons, including the price of the perpetual rotations of the Hamiltonian and the exponential storage required for the wavefunction elements, it has a property that is worthwhile to mention. If you don't encounter any excited states, you're guaranteed to eventually (i.e. after infinitely many steps) reach the ground state.

Suppose we have a state $|\Phi\rangle$. Using this state, we generate a set $\{ \hat{T}_i \}$ of transformations of the sort we've been discussing (from the Hilbert space that the Hamiltonian acts on, to a subspace fixed by a part of $|\Phi\rangle$). As we saw earlier, there will be a subspace for each $i$ which $\hat{T}_i \hat{T}_i^\dagger$ doesn't touch (it's just ones on the diagonal for those states, like an identity operator). All operators $\hat{X}_i$ that vanish outside that subspace satisfy $\hat{X}_i \hat{T}_i \hat{T}_i^\dagger = \hat{X}_i.$

The only constraint we impose on the $\hat{T}_i$ operators is that there exist operators $\hat{X}_i$ such that $\sum_{i} \hat{X}_i = \hat{1}.$ This condition can always be met if we try to update each element of $|\Phi\rangle$ at least once, which we would have to do if we wanted any chance at all of finding the ground state. Hence, the constraint is just a formality. Let's look at a concrete example:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17

julia> v = [1, 2, 3, 4, 5, 6];
julia> v /= norm(v);
julia> Ts = [make_T(v, i) for i in 1:length(v)];
julia> Xs = [zeros(length(v), length(v)) for _ in 1:length(v)];
julia> for i in 1:length(v)
           Xs[i][i, i] = 1
       end
julia> all(X*T*T' == X for (X, T) in zip(Xs, Ts))
true
julia> sum(Xs)
6×6 Array{Float64,2}:
 1.0  0.0  0.0  0.0  0.0  0.0
 0.0  1.0  0.0  0.0  0.0  0.0
 0.0  0.0  1.0  0.0  0.0  0.0
 0.0  0.0  0.0  1.0  0.0  0.0
 0.0  0.0  0.0  0.0  1.0  0.0
 0.0  0.0  0.0  0.0  0.0  1.0

It's clear that if $|\Phi\rangle$ is changed during the sweeps, its energy expectation value must go down, and if we keep that up, we'll eventually reach the ground state. However, if $|\Phi\rangle$ is a pathological state that does not change at any step of our procedure, then it must be the case that $(\hat{T}_i^\dagger \hat{H} \hat{T}_i) (\hat{T}_i^\dagger |\Phi\rangle) = E (\hat{T}_i^\dagger |\Phi\rangle)$ for all $i$, where $E = \langle\Phi|\hat{H}|\Phi\rangle.$ From this we see that $\hat{X}_i \hat{T}_i \hat{T}_i^\dagger \hat{H} |\Phi\rangle = E \hat{X}_i |\Phi\rangle,$ so $\sum_i \hat{X}_i \hat{H} |\Phi\rangle = E \sum_i \hat{X}_i |\Phi\rangle,$ which implies that $\hat{H} |\Phi\rangle = E |\Phi\rangle.$ That is, $|\Phi\rangle$ must be an eigenstate of the Hamiltonian.

For the converse, suppose that $|\Phi\rangle$ is an eigenstate of the Hamiltonian. Then it immediately follows that $(\hat{T}_i^\dagger \hat{H} \hat{T}_i) (\hat{T}_i^\dagger |\Phi\rangle) = E (\hat{T}_i^\dagger |\Phi\rangle)$ for all $i$, and we can't make any progress with our procedure.

Thus, we will get hopelessly stuck at some point if and only if we reach (or start from) an eigenstate of the Hamiltonian. If it's the ground state, congratulations! If you've somehow exactly hit one of the excited states of the Hamiltonian, you should do your best to stay indoors during thunderstorms and never play the lottery.

Matrix product states

Now that we've got the projection business down pat, we're ready for something sleek and modern: the matrix product state (MPS). My goal here is not to go into the details of how to use an MPS efficiently or to prove anything about it, so I'll only give a brief introduction. At its core, a matrix product state is a collection $\{ A^{k} \}_{k=1}^L$ of rank-3 multidimensional arrays with elements $A^{k,n_k}_{i_k,i_{k+1}}$. Note that while these arrays are typically called tensors, to the best of my knowledge, they're not tensor tensors. In particular, we make no distinction between upper and lower indices. I'm sorry if this offends your sensibilities.

If we contract these tensors along the $i$ indices (whose sizes are known as the "bond dimension"), we obtain $\sum_{i_2,i_3,\cdots,i_L} A^{1,n_1}_{i_1,i_2} A^{2,n_2}_{i_2,i_3} \cdots A^{L,n_L}_{i_L,i_{L+1}} = \left( A^{1,n_1} A^{2,n_2} \cdots A^{L,n_L} \right)_{i_1,i_{L+1}},$ which is the result of multiplying together several matrices. We'll require that the outer indices of the end tensors ($i_1$ and $i_{L+1}$) have only one value each (making them vectors in this interpretation), and we'll write the index down or not as it suits our whims. We can use this newfound freedom to rewrite the above as $\sum_{i_2,i_3,\cdots,i_L} A^{1,n_1}_{i_2} A^{2,n_2}_{i_2,i_3} \cdots A^{L,n_L}_{i_L} = A^{1,n_1} A^{2,n_2} \cdots A^{L,n_L},$ which is just a tiny bit cleaner. This is a function of the physical indices $\mathbf{n}$, so we can think of it as being a wavefunction ansatz: $\langle \mathbf{n} | \Psi \rangle = A^{1,n_1} A^{2,n_2} \cdots A^{L,n_L}.$ That was the great unveil, by the way; these are called matrix product states because they're states that are represented as products over matrices.

To muddy the waters further, we can draw the matrix product in standard tensor network notation (for $L = 8$) as In this diagram, circles represent the tensors, lines represent their indices, and connected lines are contractions over indices. For comparison, a general state $\langle \mathbf{n} | \Psi \rangle$ can be thought of as a vector with an $L$-wide multi-index (or as having L indices) and looks like a dead bug: (Yes, I'm aware that insects have only 6 legs. Bear with me here; this isn't a biology discussion.)

It's not hard to show by repeated application of the SVD that every quantum state in a finite basis can be written as an MPS. In general, the result still grows exponentially with system size, but some states (in particular ground states of some one-dimensional systems) can be efficiently represented by an MPS. In practice, we won't need to make an MPS by hand, as DMRG will take care of that for us.

Interlude: Schmidt decomposition

The Schmidt decomposition is a powerful tool in quantum mechanics. For any pure state $|\Psi\rangle$ in a bipartite Hilbert space ($\mathcal{H} = \mathcal{H}_\mathrm{A} \otimes \mathcal{H}_\mathrm{B}$), the decomposition is deceptively simple: $|\Psi\rangle = \sum_{i} \sqrt{\lambda_i} |\phi^\mathrm{A}_i\rangle |\phi^\mathrm{B}_i\rangle,$ where $\lambda_i$ are non-negative real numbers, and $\{ |\phi^\mathrm{A}_i\rangle \}_i$ and $\{ |\phi^\mathrm{B}_i\rangle \}_i$ are orthonormal bases (Schmidt bases) for $\mathcal{H}_A$ and $\mathcal{H}_B$. It's important not to confuse this with the generic basis expansion $|\Psi\rangle = \sum_{i,j} C_{i,j} |\phi^\mathrm{A}_i\rangle |\phi^\mathrm{B}_j\rangle.$ There are infinitely many such expansions in arbitrary bases, but the Schmidt decomposition is unique!

Finding the partial trace in the Schmidt decomposition turns out to be easy peasy: $\varrho_\mathrm{A} = \mathrm{Tr}_\mathrm{B} |\Psi\rangle\langle\Psi| = \sum_{i,j} \sqrt{\lambda_i \lambda_j} |\phi^\mathrm{A}_i\rangle\langle\phi^\mathrm{A}_j| \delta_{ij} = \sum_{i} \lambda_i |\phi^\mathrm{A}_i\rangle\langle\phi^\mathrm{A}_i|.$ Hence, the eigenvalues of $\varrho_\mathrm{A}$ are $\lambda_i$ and its eigenbasis is the Schmidt basis for $\mathrm{A}$.

If we write the wavefunction coefficients $\langle \mathbf{n} | \Psi \rangle$ as a matrix $M$, with those indices in $\mathrm{A}$ acting as the rows and those in $\mathrm{B}$ as the columns, then we can SVD that matrix: $M = U \Sigma V^\dagger.$ The $\Sigma$ matrix is the diagonal matrix of singular values, and $U$ and $V^\dagger$ are unitary matrices. The matrix multiplication may be drawn as the tensor contraction

One occasion when this decomposition is useful is in making an approximate state. By throwing away contributions from the smallest singular values, we reduce the size of the left and right tensors, but at the cost of making the approximation worse. We could do this truncation in many ways, but as White observed in his DMRG paper (albeit in a different language), using the Schmidt decomposition is optimal.

Matrix product operators

Operators can also be expressed as tensors in a finite basis (e.g. $\langle \mathbf{m} | \hat{O} | \mathbf{n} \rangle$) and may be expanded in a similar matrix product form, called a matrix product operator (MPO): The squares are rank-4 multidimensional arrays with elements $B^{k,m_k,n_k}_{i_k,i_{k+1}}$ (same as the tensors of an MPS, but with an additional physical index). As with states, this is the expansion of a multi-index matrix: Here all the indices (lines) on one side represent $\mathbf{m}$ and on the other represent $\mathbf{n}$.

Because an expectation value is evaluated in a basis as $\langle \Psi | \hat{O} | \Psi \rangle = \sum_{\mathbf{m},\mathbf{n}} \langle \Psi | \mathbf{m} \rangle \langle \mathbf{m} | \hat{O} | \mathbf{n} \rangle \langle \mathbf{n} | \Psi \rangle,$ we see that this is given by the contraction of an MPO with an MPS on either side:

I'll do my best not to go into too much detail here, but I should mention that there is a standard way to construct an MPO. In practice, it's often not even relevant, since ITensor can make an MPO for you automatically. Still, I think it's instructive to take a look at an MPO for an example operator. And what better example than the Hamiltonian we've been tormenting all this time?

The Hamiltonian in question, unchanged from before, is $\hat{H} = -\sigma^z_1 \sigma^z_2 - \sigma^z_2 \sigma^z_3 - \sigma^x_1 - \sigma^x_2 - \sigma^x_3.$ Conveniently, this has a regular structure: at each site we have a local term, and we also complete and start two-body terms. It's easy to see by ignoring the $\otimes$ symbols and performing the matrix multiplication that $\hat{H} = \begin{pmatrix} -\sigma_1^x & \hat{1} & -\sigma_1^z \end{pmatrix} \otimes \begin{pmatrix} \hat{1} & & \\ -\sigma_2^x & \hat{1} & -\sigma_2^z \\ \sigma_2^z & & \end{pmatrix} \otimes \begin{pmatrix} \hat{1} \\ -\sigma_3^x \\ \sigma_3^z \end{pmatrix}.$

If you're uncomfortable with putting operators into matrices, I can't blame you. What we're really doing is constructing block matrices composed of the matrix representations of these operators. Actually, that's a lie, because the result of that would be a $2 \times 2$ matrix in this example, and not the correct $8 \times 8$ matrix. What we're really doing is taking tensor products of the blocks as we do the matrix multiplication (hence the $\otimes$ symbols), but I don't know of any common notation for that. If that doesn't make any sense, maybe this will clarify matters: $\begin{pmatrix} \hat{1} & & \\ -\sigma_2^x & \hat{1} & -\sigma_2^z \\ \sigma_2^z & & \end{pmatrix} \otimes \begin{pmatrix} \hat{1} \\ -\sigma_3^x \\ \sigma_3^z \end{pmatrix} = \begin{pmatrix} \hat{1} \otimes \hat{1} \\ -\sigma_2^x \otimes \hat{1} - \hat{1} \otimes \sigma_3^x - \sigma_2^z \otimes \sigma_3^z \\ \sigma_2^z \otimes \hat{1} \end{pmatrix}$ and $\begin{pmatrix} -\sigma_1^x & \hat{1} & -\sigma_1^z \end{pmatrix} \otimes \begin{pmatrix} \hat{1} \otimes \hat{1} \\ -\sigma_2^x \otimes \hat{1} - \hat{1} \otimes \sigma_3^x - \sigma_2^z \otimes \sigma_3^z \\ \sigma_2^z \otimes \hat{1} \end{pmatrix} = \hat{H},$ where $\hat{H} = -\sigma_1^x \otimes \hat{1} \otimes \hat{1} - \hat{1} \otimes \sigma_2^x \otimes \hat{1} - \hat{1} \otimes \hat{1} \otimes \sigma_3^x - \hat{1} \otimes \sigma_2^z \otimes \sigma_3^z - \sigma_1^z \otimes \sigma_2^z \otimes \hat{1}.$

To be positively concrete, the way we construct the MPO tensors $B^k$ in the above is by treating every $B^{k}_{i_k,i_{k+1}}$ as a matrix for each pair of bond indices and filling it with the matrix elements of the corresponding one-body operator. For example, $B^{2}_{2,1} = \begin{pmatrix} 0 & -1 \\ -1 & 0 \end{pmatrix}.$ This is $2 \times 2$, because the one-body basis is two-dimensional. It's important to note that this is the inverse perspective from what one normally associates with the phrase "matrix product". One of the matrix product matrices would instead be $B^{2,1,2} = \begin{pmatrix} 0 & 0 & 0 \\ -1 & 0 & 0 \\ 0 & 0 & 0 \end{pmatrix},$ which is $3 \times 3$.

This way of constructing MPOs won't be the most compact, but it has the nice property that a single artisanal tensor $\begin{pmatrix} \hat{1} & & \\ -\sigma_k^x & \hat{1} & -\sigma_k^z \\ \sigma_k^z & & \end{pmatrix}$ is enough to generate an MPO for any number of sites. Each tensor only contains one-body operators acting on that site, and the careful placement of the operators in the matrix results in all the many-body terms of the operator. Even the end tensors can be read off from the seed tensor: they're the second row and the first column.

I think I failed at not going into the details. Since you're still here, how about another detail? If you're wondering how the tensor product comes into the picture, the MPO contraction $\sum_{i_2,i_3,\cdots,i_L} B^{1,m_1,n_1}_{i_2} B^{2,m_2,n_2}_{i_2,i_3} \cdots B^{L,m_L,n_L}_{i_L}$ implicitly does the tensor product operation, which is how we end up with a $2^3 \times 2^3$ matrix. Spooky.

D! M! R! G!

Now that we're all caught up on the circles and the squares, we can move on to the main course. We've been through a lot together now, but at some point way back when, we were finding the ground state of a Hamiltonian by tackling it in parts. Now we get to see how the MPS ansatz together with an MPO representation of the Hamiltonian allow us to do this relatively easily.

To begin, we need a trial MPS. A good place to start is with a product matrix product state: If each tensor is the ground state of the one-body problem and the coupling interaction is not too strong, you're most of the way to the final answer already! If you find the lack of lines connecting the circles distressing, don't worry, it's perfectly natural: in a product state, each matrix is just a scalar, so contraction is meaningless.

In order to update the MPS we'll need to remove a piece. We can then project the Hamiltonian onto the remaining pieces. For reasons which will become clear later on, we'll remove two tensors at once, resulting in 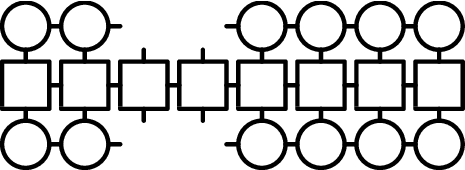(I've taken a bite out of the middle because I'm too lazy to deal with edge considerations in any of the following.) By performing all the contractions, we obtain the following rank-8 beast:

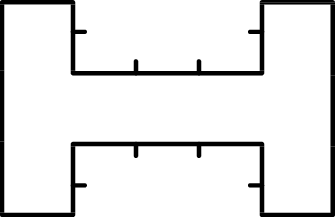
If we perform a minimization of over all possible rank-4 tensors of the appropriate size, we will have obtained the ground state in the region of Hilbert space onto which we have projected. The size is determined by the two bond dimensions (horizontal) and the two physical dimensions (vertical), which are both fixed.

It turns out that we already know a good scheme for finding the optimal tensor: iterative diagonalization. The above 8-way contraction for the expectation value may be written as $\sum_{i',m',n',j',i,m,n,j} C_{i'm'n'j'} H_{i'm'n'j';imnj} C_{imnj},$ where the notation is highly suggestive of a multi-index matrix and vector. Indeed, if we find the ground state of the matrix with elements $H_{i'm'n'j';imnj}$, we'll've obtained a vector with elements $C_{imnj}$ such that this contraction is minimized.

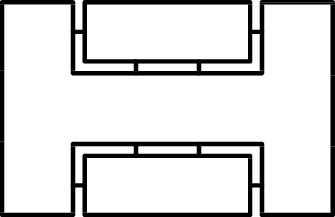
What remains is to convert the resulting rank-4 tensor into a contraction of two rank-3 tensors so that we can put them back into our MPS. Our good friend SVD comes to the rescue! As we saw earlier, we can decompose the tensor into two smaller tensors and a diagonal tensor:

We can see that if we put this piece back into our MPS and contract all the circles, we'll obtain a Schmidt decomposition for the entire state. This is then the perfect time to truncate the singular values to obtain a more compact MPS with minimal loss of accuracy. A typical strategy is to drop singular values until the discarded potion reaches a predetermined threshold: $\sum_i (\sqrt{\lambda_i})^2 = \sum_i \lambda_i \le \varepsilon.$

Finally, we contract the diagonal matrix of singular values into either side so that we're left with just two rank-3 tensors that we can insert back into the MPS. We can now see that if we only take a single site to be updated, then we wouldn't be able to do an SVD and would have no easy way to change the bond dimension of the MPS.

On the surface, that's all there is to DMRG: you pick two consecutive sites at a time, perform optimization for those two tensors, and sweep back and forth over the lattice. Of course there are many nuances that I've glossed over, but hopefully you now have a thorough understanding of why DMRG is just iterated projected iterative diagonalization.

Reference implementation

My Julia package LatticeSweeper.jl implements the above ideas (and some others) in a way that is hopefully straightforward to understand. For example, here's a snippet of the diagonalization step:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39

# The previous two-site wavefunction will be used as the starting vector:
#
#        m     n
#        |     |
#     a -#- b -#- c
@tensor prev[a, m, n, c] :=
    psi.tnsrs[site][a, m, b] * psi.tnsrs[site+1][b, n, c]

# Application of the two-site-projected Hamiltonian onto a vector:
#
#     #- c           i -#
#     #     n     p     #
#     #     |     |     #
#     #- b -#- d -#- h -#
#     #     |     |     #
#     #     m     o     #
#     #     |     |     #
#     #- a -#######- g -#
function H_f(dest::AbstractVector, src::AbstractVector)
    dest_ = reshape(dest, size(prev)...)
    src_ = reshape(src, size(prev)...)
    @tensor dest_[c, n, p, i] =
        left[a, b, c] * src_[a, m, o, g] *
        H.tnsrs[site][b, m, n, d] * H.tnsrs[site+1][d, o, p, h] *
        right[g, h, i]
    dest
end
H_map = LinearMap{T}(H_f, prod(size(prev)); issymmetric=true)

# Improve our guess for the ground state of the two-site-projected
# Hamiltonian by using a sparse diagonalizer. Since there's no way to
# request a specific number of iterations, we just say we're converged
# after a single iteration and repeat several times.
eigen = eigs(H_map; nev=1, which=:SR, tol=Inf, maxiter=1, v0=vec(prev))
wf = vec(eigen[2])
for _ in 1:(set.num_iters-1)
    eigen = eigs(H_map; nev=1, which=:SR, tol=Inf, maxiter=1, v0=wf)
    wf = vec(eigen[2])
end